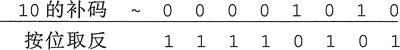位运算符(Bitwise Operators)用于在位(bit)级别操作数据,也称为位( bit ) 级别编程。
位(bit)是计算机中处理数据的最小单位,其取值只能是 0 或 1。字节(Byte)是计算机处理数据的基本单位,通常系统中一个字节为 8 位。即:1 Byte=8 bit。
位运算符分按位运算符和移位运算符。按位运算符&,|,^,~。
移位运算符: <<, >>
位移运算符可以在二进制的基础上对数字进行平移, 以加快计算过程。
以下是“ C”编程语言提供的按位运算符的列表:
| Operator (位运算符) | Meaning (意义) |
| & | Bitwise AND operator (位运算符与,按位与) |
| | | Bitwise OR operator (位运算符,按位或) |
| ^ | Bitwise exclusive OR operator (按位异或) |
| ~ | Complement Operator (位运算,一元运算符,二进制取反) |
| << | Left shift operator (位移运算符左移) |
| >> | Right shift operator (位移运算符右移) |
位运算符通常与整数数据类型一起使用,不能直接应用于其他数据类型,例如float,double等。
位逻辑运算符从最右边最低有效位LSB(least significant bit)开始,朝着最左边的最高有效位 (MSB,Most Significant Bit)对数据进行逐位处理。
下表显示了位逻辑运算符的计算结果:
| x | y | x & y | x | y | x ^ y |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 0 |
按位与 (Bitwise AND)
这是最常用的逻辑按位运算符之一。 它由单个与号(&)表示。 两个整数表达式写在(&)运算符的每一侧。
如果两个位的值均为1,则按位与运算的结果为1;否则为0。 否则,结果始终为0。
让我们考虑一下,我们有2个变量op1和op2,其值如下:
Op1 = 0000 1101 Op2 = 0001 1001
变量op1和op2的AND运算结果为
Result = 0000 1001
如我们所见,两个变量被逐位比较。 每当两个变量中的位的值均为1时,结果将为1否则为0。
按位或 (Bitwise OR)
Op1 = 0000 1101 Op2 = 0001 1001
对变量op1和op2进行按位或运算的结果将为
Result = 0001 1101
如我们所见,两个变量被逐位比较。 每当两个变量中任一位的值为1时,结果将为1否则为0。
按位异或 (Bitwise Exclusive) OR
按位异或用符号(^)表示。 在(^)运算符的每一侧都写入了两个整数表达式。
如果只有一个表达式的值为1,则按位异或运算的结果为1; 否则,结果始终为0。
让我们考虑一下,我们有2个变量op1和op2,其值如下:
Op1 = 0000 1101 Op2 = 0001 1001
按位异或运算的结果
Result=00010100
对两个变量进行逐位比较。 只有一个变量的值为1,则结果为1; 否则结果为0
示例:
#include <stdio.h>
int main()
{
int a = 20; /* 20 = 010100 */
int b = 21; /* 21 = 010101 */
int c = 0;
c = a & b; /* 20 = 010100 */
printf("AND - Value of c is %d\n", c );
c = a | b; /* 21 = 010101 */
printf("OR - Value of c is %d\n", c );
c = a ^ b; /* 1 = 0001 */
printf("Exclusive-OR - Value of c is %d\n", c );
getch();
}
移位运算符
| << | 二进制左移运算符。将一个运算对象的各二进制位全部左移若干位(左边的二进制位丢弃,右边补0)。 | 60 << 2 将得到 240,即为 1111 0000 |
| >> | 二进制右移运算符。将一个数的各二进制位全部右移若干位,正数左补0,负数左补1,右边丢弃。 | 60 >> 2 将得到 15,即为 0000 1111 |
示例:x是带有数据1111的整数表达式。执行移位运算后,结果将是:
x << 2 (left shift) = 1111<<2 = 1100 x >> 2 (right shift) = 1111>>2 = 0011
可以将移位运算符组合在一起,然后将其用于从整数表达式中提取数据。 让我们编写一个程序来演示按位移位运算符的用法。
#include <stdio.h>
int main() {
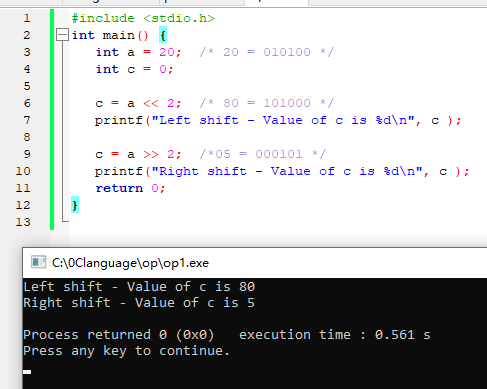
int a = 20; /* 20 = 010100 */
int c = 0;
c = a << 2; /* 80 = 1010000 */
printf("Left shift - Value of c is %d\n", c );
c = a >> 2; /*05 = 000101 */
printf("Right shift - Value of c is %d\n", c );
return 0;
}
执行左移操作后,该值将变为80,其二进制等效值为1010000。
执行右移操作后,该值将变为5,其二进制等效值为000101。
按位补码运算符 (Bitwise complement operator)
原码、反码和补码
原码:用最高位表示符号位,其余位表示数值位的编码称为原码。其中,正数的符号位为 0,负数的符号位为 1。
正数的原码、反码、补码均相同。
负数的反码:把原码的符号位保持不变,数值位逐位取反,即可得原码的反码。
负数的补码:在反码的基础上加 1 即得该原码的补码。
例如:
+11 的原码为: 0000 1011
+11 的反码为: 0000 1011
+11 的补码为: 0000 1011
-7 的原码为:1000 0111
-7 的反码为:1111 1000
-7 的补码为:1111 1001
注意,对补码再求一次补码操作就可得该补码对应的原码。
正数的补码是其本身,负数的补码为其反码加 1。 它是一元运算符。当我们对任何位执行取反操作时,所有1都变为0,反之亦然。
如果我们有一个包含0000 1111的整数表达式,那么在执行取反运算后,该值将变为1111 0000。
按位取反运算符用代字号(〜)表示。
应用:~a+1=-a 即对任意数按位取反后加 1,得该数的相反数。
例如,计算 10 按位取反的结果,如下所示:
由于计算机中位运算均是以补码形式操作的,正数的补码是其本身,负数的补码为其反码加 1。
所得显然是负数的补码,对补码 1111 0101 再做一次求补操作,即可得该补码对应的原码。 求 1111 0101 补码的过程如下所示:
反码 1000 1010 –符号位 1 保持不变,数值位按位取反
补码 1000 1011 –反码加1
根据 (补码)补码=原码
故补码1111 0101对应的原码为1000 1011=-11,即:~(10)D =~(0100 0110)B补= (1111 0101)B补=-11
由此可见,~10+1=-11+1=-10,即满足 ~a+1=-a
让我们编写一个程序来演示按位补码运算符的实现:
#include <stdio.h>
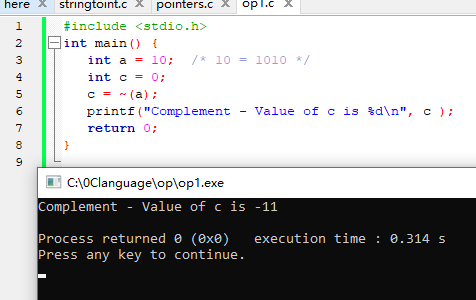
int main() {
int a = 10; /* 10 = 1010 */
int c = 0;
c = ~(a);
printf("Complement - Value of c is %d\n", c );
return 0;
}
按位运算符和移位运算符详细举例:
#include <stdio.h>
main() {
unsigned int x = 48; /* 48 = 0011 0000 */
unsigned int y = 13; /* 13 = 0000 1101 */
int z = 0;
z =x & y; /* 0 = 0000 0000 */
printf("Bitwise AND Operator - x & y = %d\n", z );
z = x | y; /* 61 = 0011 1101 */
printf("Bitwise OR Operator - x | y = %d\n", z );
z= x^y; /* 61 = 0011 1101 */
printf("Bitwise XOR Operator- x^y= %d\n", z);
z = ~x; /*-61 = 1100 0011 */
printf("Bitwise One's Complement Operator - ~x = %d\n", z);
z = x << 2; /* 192 = 1100 0000 */
printf("Bitwise Left Shift Operator x << 2= %d\n", z );
z= x >> 2; /* 12 = 0000 1100 */
printf ("Bitwise Right Shift Operator x >> 2= %d\n", z );}
负数的二进制表示
我们已经知道计算机中,所有数据最终都是使用二进制数表达。
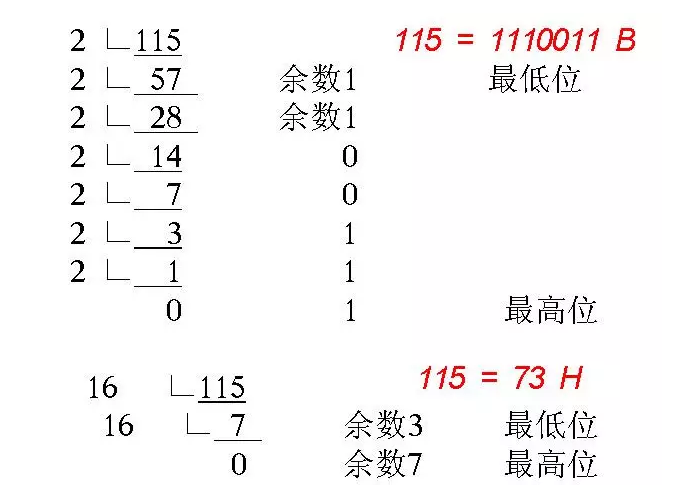
我们也已经学会如何将一个10进制数如何转换为二进制数以及如何将如何将一个16进制数如何转换为二进制数,详见下图。
不过,我们仍然没有学习一个负数如何用二进制表达。
比如,假设有一 int 类型的数,值为5,那么,我们知道它在计算机中表示为:00000000 00000000 00000000 00000101
5转换成二制是101,不过int类型的数占用4字节(32位),所以前面填了一堆0。
现在想知道,-5在计算机中如何表示?
在计算机中,负数以其正值的补码形式表达
什么叫补码呢?这得从原码,反码说起。
原码:一个整数,按照绝对值大小转换成的二进制数,称为原码。
比如 00000000 00000000 00000000 00000101 是 5的 原码。
反码:将二进制数按位取反,所得的新二进制数称为原二进制数的反码。
取反操作指:原为1,得0;原为0,得1。(1变0; 0变1)
比如:将00000000 00000000 00000000 00000101每一位取反,得11111111 11111111 11111111 11111010。
称:11111111 11111111 11111111 11111010是 00000000 00000000 00000000 00000101 的反码。
反码是相互的,所以也可称:
11111111 11111111 11111111 11111010 和00000000 00000000 00000000 00000101 互为反码。
补码:反码加1称为补码。
也就是说,要得到一个数的补码,先得到反码,然后将反码加上1,所得数称为补码。
比如:00000000 00000000 00000000 00000101的反码是:11111111 11111111 11111111 11111010。
那么,补码为:
11111111 11111111 11111111 11111010 + 1 = 11111111 11111111 11111111 11111011
所以,-5 在计算机中表达为:11111111 11111111 11111111 11111011。
转换为十六进制:0xFFFFFFFB。
再举一例,我们来看整数-1在计算机中如何表示。
假设这也是一个int类型,那么:
1、先取1的原码:00000000 00000000 00000000 00000001
2、得反码: 11111111 11111111 11111111 11111110
3、得补码: 11111111 11111111 11111111 11111111
可见,-1在计算机里用二进制表达就是全1。16进制为:0xFFFFFF。